B2. Act. 28. División. Decimal y fracción. 1/12/16
Tema. División con decimal y fracción.
Para resolver este tipo de operaciones se debe convertir alguno de ellos para tener sólo fracciones o decimales.
Posteriormente se aplican los pasos previamente explicados para operaciones con fracciones y operaciones con decimales.
Actividad. Resuelve las siguientes operaciones respetando los pasos indicados en las previamente.
6/9:.4=
.8:3/9=
.25:3/8=
1.2:8/5=
6/4:.9=
2.4:2/3=
.25:5/3=
5/8:.11=
martes, 29 de noviembre de 2016
B2. Act. Multiplicación. Decimal y fracciones. 30/11/16
B2. Act. Multiplicación. Decimal y fracciones. 30/11/16
Tema. Multuplicación con decimal y fracción.
Para resolver este tipo de operaciones se debe convertir alguno de ellos para tener sólo fracciones o decimales.
Posteriormente se aplican los pasos previamente explicados para operaciones con fracciones y operaciones con decimales.
Actividad. Resuelve las siguientes operaciones respetando los pasos indicados en las previamente.
5/6*.05=
3.7*1/6=
2/3*.25=
5/6*.75=
7/9*.12=
.8*1/7=
.75*1/5=
4/8*.33=
1.34*5/6=
2/3*.68=
Tema. Multuplicación con decimal y fracción.
Para resolver este tipo de operaciones se debe convertir alguno de ellos para tener sólo fracciones o decimales.
Posteriormente se aplican los pasos previamente explicados para operaciones con fracciones y operaciones con decimales.
Actividad. Resuelve las siguientes operaciones respetando los pasos indicados en las previamente.
5/6*.05=
3.7*1/6=
2/3*.25=
5/6*.75=
7/9*.12=
.8*1/7=
.75*1/5=
4/8*.33=
1.34*5/6=
2/3*.68=
B2. Act. 26. Área. 29/11/16
B2. Act. 26. Área. 29/11/16
Actividad. Calcula el área de cada figura de acuerdo a las medidas proporcionadas.
Cuadrado. 3.5cm
Cuadrado. 7.5cm
Rectángulo. Base 17cm, altura 23cm
Rectángulo. Base 43cm, altura 79cm
Triángulo. Base 12.4cm, altura 17.1cm
Triángulo. Base 11.6cm, altura 7.4cm
Rombo. Diagonal mayor 23cm, diagonal menor 14cm
Romboide. Base 4.6cm, altura 5.3cm
Trapecio. Base mayor 4cm, base menor 2.5cm, altura 3cm
Círculo. Radio 2.1cm
Pentágono. Lado 5cm, apotema 4.5cm
Actividad. Calcula el área de cada figura de acuerdo a las medidas proporcionadas.
Cuadrado. 3.5cm
Cuadrado. 7.5cm
Rectángulo. Base 17cm, altura 23cm
Rectángulo. Base 43cm, altura 79cm
Triángulo. Base 12.4cm, altura 17.1cm
Triángulo. Base 11.6cm, altura 7.4cm
Rombo. Diagonal mayor 23cm, diagonal menor 14cm
Romboide. Base 4.6cm, altura 5.3cm
Trapecio. Base mayor 4cm, base menor 2.5cm, altura 3cm
Círculo. Radio 2.1cm
Pentágono. Lado 5cm, apotema 4.5cm
domingo, 27 de noviembre de 2016
B2. Act. 25. Área. 28/11/16
B2. Act. 25. Área. 28/11/16
Actividad. Calcula el área de las siguientes figuras aplica correctamente la fórmula para cada una.
Actividad. Calcula el área de las siguientes figuras aplica correctamente la fórmula para cada una.
Cuadrado. 3.5cm
Cuadrado. 7.5cm
Cuadrado. 7.5cm
Rectángulo. Base 17cm, altura 23cm
Rectángulo. Base 43cm, altura 79cm
Rectángulo. Base 43cm, altura 79cm
Triángulo. Base 12.4cm, altura 17.1cm
Triángulo. Base 11.6cm, altura 7.4cm
Triángulo. Base 11.6cm, altura 7.4cm
Rombo. Diagonal mayor 23cm, diagonal menor 14cm
Rombo. Diagonal mayor 15.2cm, diagonal menor 10.9cm
Rombo. Diagonal mayor 15.2cm, diagonal menor 10.9cm
Romboide. Base 4.6cm, altura 5.3cm
Romboide. Base 8.5cm, altura 1.4cm
Trapecio. Base mayor 4cm, base menor 2.5cm, altura 3cm
Trapecio. Base mayor 2.5cm, base menor 2.1cm, altura 1.5 cm
Círculo. Radio 13.4cm
Círculo. Radio 21.2cm
Pentágono. Lado 5cm, apotema 3.5cm
Pentágono. Lado 6cm, apotema 5.5cm
Pentágono. Lado 6cm, apotema 5.5cm
miércoles, 23 de noviembre de 2016
B2. Act. 24. Área. 23/11/16
B2. Act. 24. Área. 23/11/16
Área.
Actividad. Calcula el área de las siguientes figuras.
Área.
Actividad. Calcula el área de las siguientes figuras.
Trapecio. Base mayor 40cm, base menor 25cm, altura 30cm
Trapecio. Base mayor 25cm, base menor 20cm, altura 15 cm
Círculo. Radio 20cm
Círculo. Radio 15cm
Pentágono. Lado 50cm, apotema 30cm
Pentágono. Lado 15cm, apotema 13cm
Pentágono. Lado 15cm, apotema 13cm
B2. Act. 23. Área. 22/11/16
B2. Act. 23. Área. 22/11/16
Tema. Áreas.
El área es la medida de una superficie en unidades cuadradas (mm², cm², m², km², etc.).
El resultado al calcular una área se puede interpretar como la cantidad de cuadros que caben en la superficie de una figura.
Ejemplo 1.
En este ejemplo ocurre lo mismo el cuadrado tiene 4 centímetros de lado, por lo tanto su área será 16cm ²
Ejemplo 3.
En este último ejemplo podemos observar que el área es de un centímetro cuadrado (la de color rojo), sin embargo, podemos marcar el área en milímetros (de color azul).
Para calcular el área se debe conocer la fórmula de cada figura.
Actividad. Calcula el área de las siguientes figuras.
Tema. Áreas.
El área es la medida de una superficie en unidades cuadradas (mm², cm², m², km², etc.).
El resultado al calcular una área se puede interpretar como la cantidad de cuadros que caben en la superficie de una figura.
Ejemplo 1.
Si tengo un rectángulo que mide 5cm de base por 2cm de altura. Su área es 10 cm².
Eso significa que dentro de ese rectángulo caben 10 cuadrados que miden un centímetro de cada lado.
Ejemplo 2.
En este ejemplo ocurre lo mismo el cuadrado tiene 4 centímetros de lado, por lo tanto su área será 16cm ²
Ejemplo 3.
En este último ejemplo podemos observar que el área es de un centímetro cuadrado (la de color rojo), sin embargo, podemos marcar el área en milímetros (de color azul).
Para calcular el área se debe conocer la fórmula de cada figura.
Actividad. Calcula el área de las siguientes figuras.
Cuadrado. 8cm
Cuadrado. 25cm
Cuadrado. 25cm
Rectángulo. Base 30cm, altura 50cm
Rectángulo. Base 40cm, altura 60cm
Rectángulo. Base 40cm, altura 60cm
Triángulo. Base 35cm, altura 40cm
Triángulo. Base 60cm, altura 30cm
Triángulo. Base 60cm, altura 30cm
Rombo. Diagonal mayor 48cm, diagonal menor 38cm
Rombo. Diagonal mayor 70cm, diagonal menor 50cm
Rombo. Diagonal mayor 70cm, diagonal menor 50cm
Romboide. Base 64cm, altura 35cm
Romboide. Base 58cm, altura 41cm
viernes, 18 de noviembre de 2016
B2. Act. 22. Perímetro. 18/11/16
B2. Act. 22. Perímetro. 18/11/16
Tema. Cálculo del perímetro.
El perímetro es la suma de todas las medidas de los lados de una figura.
Para obtenerlo se suman todos los lados sin olvidar colocar la magnitud indicada (es decir, si son cm, m, km,etc.)
Ejemplo.
Cuál es el perímetro de las siguientes figuras.
Tema. Cálculo del perímetro.
El perímetro es la suma de todas las medidas de los lados de una figura.
Para obtenerlo se suman todos los lados sin olvidar colocar la magnitud indicada (es decir, si son cm, m, km,etc.)
Ejemplo.
Cuál es el perímetro de las siguientes figuras.
10+10+10+10+3+7+4+5= 59 cm
6+5+6+5= 22cm
Actividad. Crea 10 polígonos simples irregulares, mide y anota sus lados, además de obtener el perímetro para cada una.
B2. Act. 21. Examen. 18/11/16
B2. Act. 21. Examen. 18/11/16
Actividad. Examen pegado y firmado por el padre o tutor.
Actividad. Examen pegado y firmado por el padre o tutor.
B2. Act. 20. Formulario. 16/11/16
B2. Act. 20. Formulario. 16/11/16
Actividad. Elabora el formulario de los temas:
Polígono
Polígono simple
Polígono compuesto
Polígono regular
Polígono irregular
Vértice
Arista
Construcción de ángulos
Ángulos internos
Ángulos externos
Actividad. Elabora el formulario de los temas:
Polígono
Polígono simple
Polígono compuesto
Polígono regular
Polígono irregular
Vértice
Arista
Construcción de ángulos
Ángulos internos
Ángulos externos
B2. Act. 19. Ángulos externos. 15/11/16
B2. Act. 19. Ángulos externos. 15/11/16
Tema. Cálculo de la medida de los ángulos externos de un polígono.
Como el nombre lo indica los ángulos externos de un polígono son los que se forman fuera de su perímetro.
Para hacer el cálculo correcto se debe extender la línea recta de una de las aristas, esto servirá para medir los grados el ángulo externo.
Recuerda que siempre el ángulo exterior sumado con el ángulo interior sumarán 180 grados.
Para calcular la medida del ángulo debe alinearse la marca del transportador con el vértice y la arista del ángulo que se desea medir.
Recuerda aplicar el procedimiento que utilizaste para medir ángulos en los segmentos AB, de las actividades anteriores.
Ejemplos.
Tema. Cálculo de la medida de los ángulos externos de un polígono.
Como el nombre lo indica los ángulos externos de un polígono son los que se forman fuera de su perímetro.
Para hacer el cálculo correcto se debe extender la línea recta de una de las aristas, esto servirá para medir los grados el ángulo externo.
Recuerda que siempre el ángulo exterior sumado con el ángulo interior sumarán 180 grados.
Para calcular la medida del ángulo debe alinearse la marca del transportador con el vértice y la arista del ángulo que se desea medir.
Recuerda aplicar el procedimiento que utilizaste para medir ángulos en los segmentos AB, de las actividades anteriores.
Ejemplos.
Actividad. Construye 10 polígonos irregulares y calcula la medida de sus ángulos externos.
B2. Act. 18. Ángulos internos. 14/11/16
B2. Act. 18. Ángulos internos. 14/11/16
Tema. Cálculo de la medida de los ángulos internos de un polígono.
Como el nombre lo indica los ángulos internos de un polígono son los que se forman dentro de su perímetro.
Para calcular la medida del ángulo debe alinearse la marca del transportador con el vértice y la arista del ángulo que se desea medir.
En caso de que el ángulo sea mayor de 180° simplemente se deben sumar los grados que hacen falta hasta donde se separan las aristas.
Recuerda aplicar el procedimiento que utilizaste para medir ángulos en los segmentos AB, de las actividades anteriores.
Ejemplo.
Actividad. Construye 10 polígonos irregulares y mide sus ángulos internos.
Tema. Cálculo de la medida de los ángulos internos de un polígono.
Como el nombre lo indica los ángulos internos de un polígono son los que se forman dentro de su perímetro.
Para calcular la medida del ángulo debe alinearse la marca del transportador con el vértice y la arista del ángulo que se desea medir.
En caso de que el ángulo sea mayor de 180° simplemente se deben sumar los grados que hacen falta hasta donde se separan las aristas.
Recuerda aplicar el procedimiento que utilizaste para medir ángulos en los segmentos AB, de las actividades anteriores.
Ejemplo.
Actividad. Construye 10 polígonos irregulares y mide sus ángulos internos.
viernes, 11 de noviembre de 2016
B2. Act. 17. Construcción de polígonos. 11/11/16
B2. Act. 17. Construcción de polígonos. 11/11/16
Tema. Creación de polígonos a partir de su ángulo central.
Los pasos para crear un polígono desde su ángulo central son:
Observa las imagenes.
Actividad. Crea los siguientes polígonos a partir de su ángulo central.
5 lados, 6 lados, 7 lados y 8 lados.
Tema. Creación de polígonos a partir de su ángulo central.
Los pasos para crear un polígono desde su ángulo central son:
- Se marca un punto que servirá de centro en nuestra figura.
- Se dividirá 360 entre la cantidad de lados que tendrá nuestro polígono regular.
- El resultado de esta división será la medida del ángulo central de acuerdo a la cantidad se realizarán las marcas que serán los vértices en nuestra figura.
- Las marcas se unirán cuidando que cada una esté a la misma distancia desde el centro de la figura para que resulte un polígono regular.
Observa las imagenes.
Actividad. Crea los siguientes polígonos a partir de su ángulo central.
5 lados, 6 lados, 7 lados y 8 lados.
miércoles, 9 de noviembre de 2016
B2. Act. 16. Creación de triángulos. 9/11/16
B2. Act. 16. Creación de ángulos. 9/11/16
Actividad. Crea los segmentos y los ángulos indicados para cada caso. Las medidas de los segmentos están en centímetros.
Actividad. Crea los segmentos y los ángulos indicados para cada caso. Las medidas de los segmentos están en centímetros.
B2. Act. 15. Construcción de ángulos. 8/11/16
B2. Act. 15. Construcción de ángulos. 8/11/16
Actividad. Crea los siguientes ángulos de acuerdo a las medidas proporcionadas.
Segmento AB 4.5 cm. Ángulo B 145 grados. Segmento BC 3 cm ángulo C 75°. Segmento CD 5cm
Segmento AB 3.5 cm. Ángulo B 125 grados. Segmento BC 3.5 cm. Ángulo C 80°. Segmento CD 3cm
Segmento AB 2.5 cm. Ángulo B 130 grados. Segmento BC 3 cm. Ángulo C 110°. Segmento CD 4cm
Segmento AB 4 cm. Ángulo B 155 grados. Segmento BC 3.5cm. Ángulo C 120°. Segmento CD 2.5cm
Segmento AB 5 cm. Ángulo B 165 grados. Segmento BC 4cm. Ángulo C 135°. Segmento CD 1.5cm
Actividad. Crea los siguientes ángulos de acuerdo a las medidas proporcionadas.
Segmento AB 4.5 cm. Ángulo B 145 grados. Segmento BC 3 cm ángulo C 75°. Segmento CD 5cm
Segmento AB 3.5 cm. Ángulo B 125 grados. Segmento BC 3.5 cm. Ángulo C 80°. Segmento CD 3cm
Segmento AB 2.5 cm. Ángulo B 130 grados. Segmento BC 3 cm. Ángulo C 110°. Segmento CD 4cm
Segmento AB 4 cm. Ángulo B 155 grados. Segmento BC 3.5cm. Ángulo C 120°. Segmento CD 2.5cm
Segmento AB 5 cm. Ángulo B 165 grados. Segmento BC 4cm. Ángulo C 135°. Segmento CD 1.5cm
domingo, 6 de noviembre de 2016
B2. Act. 14. Construcción de triángulos. 7/11/16
B2. Act. 14. Construcción de triángulos. 7/11/16
Tema. Construcción de ángulos.
1. Se traza un segmento (línea recta) marcando el punto A y el punto B.
2. coloca tu transportador en el punto A o en el punto B según te indiquen.
3. Cuenta y marca los grados indicados para que te traces una línea desde el vértice que usaste hacia la marca de los grados que contaste.
Observa los ejemplos.
Ángulo de 26 grados desde el punto A.
Ángulo de 135 grados desde el punto A.
Actividad.
1. Crea los siguientes ángulos desde el punto A.
50, 45, 72, 81, 93, 105, 48, 36, 49, 73.
2. Crea los siguientes ángulos desde el punto B.
150, 96, 58, 79, 75, 140, 169, 156, 76, 43.
Tema. Construcción de ángulos.
1. Se traza un segmento (línea recta) marcando el punto A y el punto B.
2. coloca tu transportador en el punto A o en el punto B según te indiquen.
3. Cuenta y marca los grados indicados para que te traces una línea desde el vértice que usaste hacia la marca de los grados que contaste.
Observa los ejemplos.
Ángulo de 26 grados desde el punto A.
Ángulo de 135 grados desde el punto A.
Actividad.
1. Crea los siguientes ángulos desde el punto A.
50, 45, 72, 81, 93, 105, 48, 36, 49, 73.
2. Crea los siguientes ángulos desde el punto B.
150, 96, 58, 79, 75, 140, 169, 156, 76, 43.
viernes, 4 de noviembre de 2016
B2. Act. 13. Polígono regular e irregular. 4/11/16
B2. Act. 13. Polígono regular e irregular. 4/11/16
Tema. Polígono regular e irregular.
Polígono regular. Es aquella figura en la que todos sus lados o aristas miden lo mismo y también sus ángulos miden lo mismo.

Polígono irregular. Es aquella figura en la que por lo menos uno de sus lados o aristas es diferente al de los otros, de la misma forma por lo menos uno de sus ángulos tiene diferente medida a los otros.
Nota. Para que se considere un polígono debe estar formado por líneas rectas si alguna línea es curva deja de ser polígono. También todas las líneas deben estar unidas si hay una separación deja de ser polígono.
Actividad. Elabora 10 polígonos irregulares. Usa regla y transportador.
Tema. Polígono regular e irregular.
Polígono regular. Es aquella figura en la que todos sus lados o aristas miden lo mismo y también sus ángulos miden lo mismo.

Polígono irregular. Es aquella figura en la que por lo menos uno de sus lados o aristas es diferente al de los otros, de la misma forma por lo menos uno de sus ángulos tiene diferente medida a los otros.
Nota. Para que se considere un polígono debe estar formado por líneas rectas si alguna línea es curva deja de ser polígono. También todas las líneas deben estar unidas si hay una separación deja de ser polígono.
Actividad. Elabora 10 polígonos irregulares. Usa regla y transportador.
B2. Act. 12. Polígono simple y complejo. 3/11/16
B2. Act. 12. Polígono simple y complejo. 3/11/16
Tema. Partes de un polígono.
Vértice. Es el punto donde se unen dos líneas rectas.
Arista. Es cada una de las líneas rectas de una figura, también conocidas como lado.
Ángulo. Es la medida de separación en grados entre dos aristas.
Tema. Polígonos simples y complejos.
Un polígono simple es aquél en donde ninguno de sus lados se cruza o encima con otro.

Ejemplo de polígono simple, ningún lado se cruza.
Un polígono complejo es aquél en el que por lo menos uno de sus lados o aristas se cruza encima con otra u otras
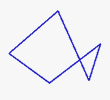
Ejemplo de polígono complejo, uno de sus lados o aristas se cruza con otro.
Actividad. Construye 7 polígonos simples y 7 polígonos complejos.
Tema. Partes de un polígono.
Vértice. Es el punto donde se unen dos líneas rectas.
Arista. Es cada una de las líneas rectas de una figura, también conocidas como lado.
Ángulo. Es la medida de separación en grados entre dos aristas.
¿Es un polígono?
Los polígonos son formas bidimensionales. LoEstán hechos con líneas rectas, y su forma es "cerrada" (todas las líneas están conectadas).
 |  | 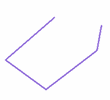 |
| Polígono (lados rectos) | No es un polígono (tiene una curva) | No es un polígono (abierto, no cerrado) |
Tema. Polígonos simples y complejos.
Un polígono simple es aquél en donde ninguno de sus lados se cruza o encima con otro.

Ejemplo de polígono simple, ningún lado se cruza.
Un polígono complejo es aquél en el que por lo menos uno de sus lados o aristas se cruza encima con otra u otras

Ejemplo de polígono complejo, uno de sus lados o aristas se cruza con otro.
Actividad. Construye 7 polígonos simples y 7 polígonos complejos.
Suscribirse a:
Entradas (Atom)
























.jpg)





